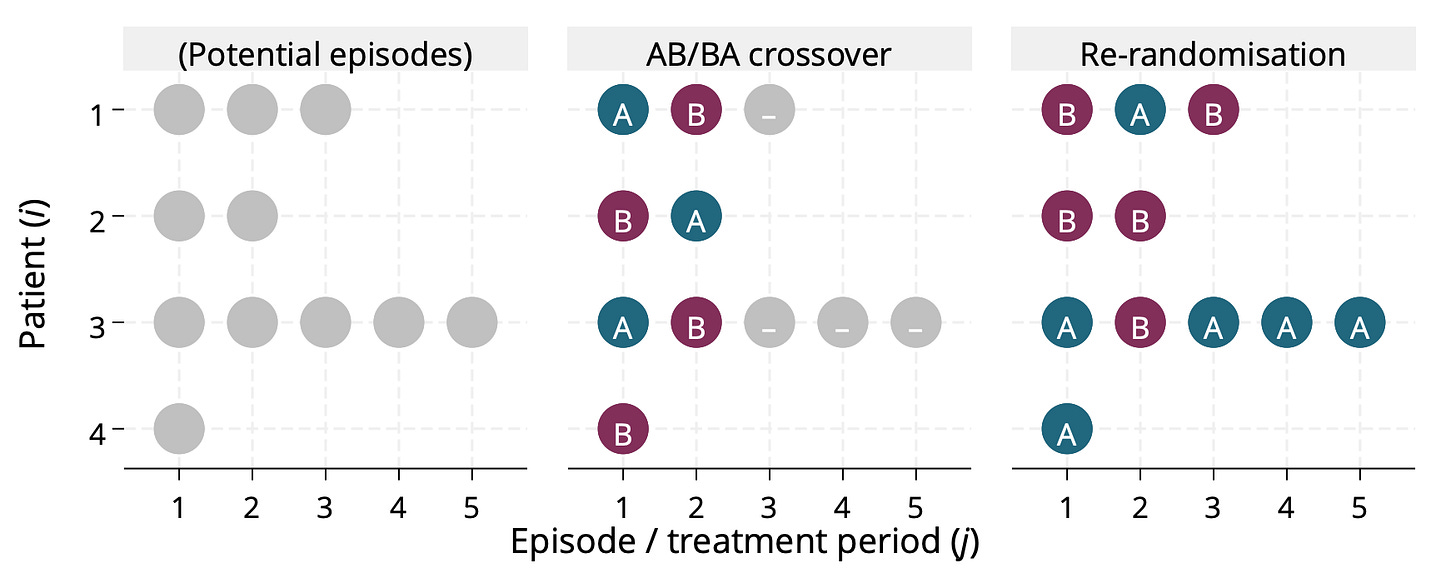
Intuitive understanding of the re-randomisation design
It’s certainly ‘wrong’ from the perspective I was taught!
The re-randomisation design in brief
The re-randomisation design allows individuals to participate in a study more than once and be randomised each time they participate. They must have completed follow-up for any previous periods before being re-randomised. The individuals’ needs, rather than the design, dictates how many periods of participation each individual contributes, so individuals will have different numbers of randomised periods. It’s crucial that they are not forced to switch from or to stick with their previously randomised treatment. The analysis does not necessarily adjust for participant; in fact, using mixed models for this purpose can induce serious bias (see the appendix additional file).
If this goes against what you think is acceptable in a trial design, this post aims to give you some intuition.
Where does it come from?
I was arguably taught1 what you might call a ‘model-based’ perspective on medical statistics. Use a certain model for a certain type of outcome, and interpret parameters of the model – hello hazard ratios! By the time I got to my MSc dissertation, Mike Kenward made sure I learned that it makes more sense to start with an estimand of scientific interest and then to find a suitable estimator. For this section, however, I’m going to approach it from a model-based perspective because if you too learned that way, that’s how I plan to talk you round.
We all get taught about how important it is to account for ‘clustering’ in statistical analysis. So in an experimental context, you might get taught that:
You have to account for ‘cluster’ in cluster-randomised designs, because outcomes are correlated within clusters
You have to account for person in crossover designs, because outcomes are correlated within individuals
You have to account for person when a longitudinal outcome is repeatedly measured over time, because again outcomes are correlated within individuals
It’s true that you need to account for clustering in these situations, but the text after ‘because’ in each line isn’t really the reason.
Why is the need to adjust for clustering not really about the correlated outcomes?
The trick here is to notice the following about the above bullets. In the cluster randomised design, everyone in a cluster is randomised to the same thing. In the crossover design they are randomised to get each thing once, so always switch. In the longitudinal design they are randomised to one thing which is the same at each outcome measurement time. In short, there is a specific restriction on randomisation according to the clusters.
Suppose we are planning a randomised controlled trial with two arms. It’s a multicentre study. We can safely assume that outcomes are positively correlated within centre (as assumed in the bulleted situations above). We could randomise individuals in one of three ways:
Simple randomisation
Block randomisation within centre
Centre randomisation (randomise the centres rather than the individuals, so that all individuals within a centre are allocated the same intervention)
In situations 2 and 3, it is necessary to account for centres at the analysis stage. In situation 1, it’s not necessary, though might be helpful. My first paper with Brennan Kahan was roughly about understanding this in situation 2, which wasn’t obvious to us. The point is that it is not about the correlation among outcomes within a centre and is in fact about the design.2
Suppose now that each of those centres contained exactly two participants. Or that instead of centres with two participants, each ‘centre’ was a married couple. Or that instead of a married couple it was one person who had two episodes of some condition. In all these cases we would expect correlation outcomes. We could randomise in one of three ways:
Simple randomisation
Crossover
Person-level randomisation (always stick with initially randomised treatment)
This closely mimics the multicentre trial situation. Let’s say we go with option 1. In the multicentre trial situation under option 1, we could safely ignore centre during the analysis. Similarly, we can ignore person in the analysis here. If you’re happy with this, you’re happy with one aspect of the re-randomisation design.
If you’re not happy with this, it’s a bit like when we have a parallel group trial with some unmeasured covariate U. We know that randomisation means we can (usually) safely ignore U. If you’re not happy with trials being able to ignore an unmeasured covariate, you’re probably one of the main characters from one of those debacles and please stop reading now. BTW, if you’re unconvinced, please do articulate what is different about the two situations in the comments.
The next odd aspect
Another aspect of the re-randomisation design is the fact that a person can participate multiple times. Oh no, we lose the lovely balance that makes crossover trials so neat! Again, look back at the multicentre trial example. Did we need to specify that every centre be exactly the same size? No. If the centres are different sizes, does it matter if we ignore them in the anaysis? Also no.
If we had a multicentre trial where each centre was forced to be the same size, then it might have some nice statistical properties but from an estimands perspective it would look very odd. One attribute of an estimand is the target population. A trial that is forced to recruit equal numbers of participants from centres in (say) Basel and Tokyo might have an implicit target population in which future-Basel and future-Tokyo will have the same number of patients. If they don’t, the targets the wrong target population. (I’m running out of steam a bit here so not explaining why.)
Viewed from this perspective, crossover trials might seem a little odd. In the AB/BA design, each trial participant has two treatment periods and gets each treatment. This is parallel to making each centre the same size. What if the condition is one in which patients have different numbers of episodes, like sickle cell crises or acute liver failure? Is this not an odd thing to do?
You probably anticipated that this would go to estimands
Brennan Kahan and colleagues have a nice paper that sets out four different estimands we might be interested in for repeated episode trials and considers estimation of these. I should re-read it but my memory is that crossover trials sometimes target these estimands under certain assumptions (e.g. non-informative cluster size), and can then be efficient. I say ‘can be’ because they may also lose information from individuals who would participate more than the two times permitted by the design. Here’s a picture.
Brief note: when you say crossover trial, most people think of a two-period, two-treatment ‘AB/BA’ design3. There are of course crossover designs with more treatments, more periods and different sequences (Balaam’s design for example permits sequences AA, AB, BA, BB). In that sense the re-randomisation is arguably a particular type of crossover design. I once said this in a presentation and Mike Kenward picked me up on it, arguing that it’s just an inefficient crossover design. I argued that there are two things that make re-randomisation distinct. First, the analysis part above (which Mike didn’t buy). Second, the fact that the design does not dictate the number of times and individual participants (which he did agree makes it different to any crossover design; of course others might not buy this).
Incidentally, over the past few years I’ve become less sympathetic towards (possibly a caricature of) design-of-experiments approaches because I’ve become more influenced by estimands and the approaches I’ve seen in causal epidemiology. This is by no means universal, but lots of DoE seems to think about efficient designs without first defining relevant, defensible estimands. This is the wrong way round because:
The estimand of interest does not depend on the study design.
The design will restrict the set of estimands you can consider.
So choosing a design/analysis combination for its efficiency risks targeting the wrong estimand. It may be that better efficiency comes from targeting a different estimand, which sometimes happens. So broadly, you should only compare efficiency for the same estimand4.
Don’t forget phases
I like the idea of the re-randomisation design but haven’t worked on it in recent years. I also like the idea of phases of development for statistical methodology, and this applies to designs as well as analyses. It would bear thinking about how to move re-randomisation forward in terms of its phase, to make it a more mature design that’s better understood (particularly when it’s not a good option, beyond the obvious cases like outcome of death5). Your thoughts on this are very welcome.
Maybe unfair to those who taught me. Possibly more accurate to say this is what I learned, possibly because I found it an easier way to view things.
You’re thinking actually it’s a little bit about the correlation, and you’re right: the design point only matters if the correlation is non-zero. Since we would almost never know this, and testing would be very silly, let’s just focus on the fact that the design dictates whether or not non-zero correlation would matter.
At the 2023 IBS CEN conference in Basel, Stephen Senn pointed out that this is a type of fractional factorial design, which I hadn’t appreciated before.
Actually it’s fine if you have more than one candidate estimand of equal interest and want to pick the one whose relative efficiency is highest.
Brennan Kahan read this and commented that re-randomisation design can in fact be a great option when you’re studying a terminal outcome like death or successful fertility treatment. Don’t know