Is multiple imputation making up information?

More like making down information

Back in the 90s, when its development went beyond “phase I”¹, one of the concerns about multiple imputation was that it is “making up data”. In a trivial sense, multiple imputation is making in data. The clue is in the name: it literally fills in missing values. This is probably not the concern, which might be better articulated as “is multiple imputation making up information?” This would indeed be concerning. Early in my PhD (on multiple imputation), I came across a paper by Joseph Schafer with a helpful answer²:

When MI is presented to a new audience, some may view it as a kind of statistical alchemy in which information is somehow invented or created out of nothing. This objection is quite valid for single-imputation methods, which treat imputed values no differently from observed ones. MI, however, is nothing more than a device for representing missing-data uncertainty. Information is not being invented with MI any more than with EM or other well accepted likelihood-based methods, which average over a predictive distribution for Y_mis by numerical techniques rather than by simulation.

– Schafer, 1999

People have asked me this question plenty of times, particularly at missing data courses. At some point, I tried the following explanation. Suppose we have access to a fully-observed dataset, and – even less realistically – know the model that generated it. We go ahead and analyse the data using this model. Next, we add some completely empty rows of data, perform multiple imputation with a correctly specified imputation model, and analyse using Rubin’s rules. The resulting inference would be no more efficient than the inference without the empty row. This would be true however many empty rows we add.

I tried this explanation when put on the spot, but was pleased enough with it to repeat subsequently. In chapter 14 of our book on multiple imputation³, the first question in the exercises is to consider the objection “multiple imputation is ‘making up data’,” and essentially discuss it.

Below, I want to show this in action with a small simulation study, because ii) I think it’s useful reassurance beyond my claiming it, and ii) I haven’t done a simulation study for a while. But first I want to mention the fraction of missing information.

Fraction of missing information (FMI)

We tend to say that multiple imputation is rarely the best thing to do, but is often close enough and readily implemented. Actually, in one context, I think it is currently the best thing; see this post. It is an odd hybrid of frequentist and Bayesian. For frequentists/likelihoodists, it approximates direct likelihood approaches with additional Monte Carlo error; for Bayesians, it’s an impoverished version of a Bayesian model for the missing and observed data. Still, there are some neat features of multiple imputation. For example, you actually get to inspect what you’ve imputed and ask whether it’s reasonable. We can use that to criticise your imputation model. Is it ok that I’ve imputed out of observable range and so on. We can also estimate quantities like FMI: the information we lost due to missing data.

Simulation study

Here’s the simulation study. I know it’s a blog post but still, ADEMPI.

Aim

To empirically investigate the amount of information added/lost by multiple imputation when there is no information in the empty rows and the imputation model is correctly specified.

Data-generating mechanism

We are going to have three variables: quantitative Y and X, and a binary Z. For n_obs=500 rows of data, first generate:

\(\begin{align} \begin{bmatrix} Y\\ X \end{bmatrix} & \sim \mathcal{N}\left(\begin{bmatrix} 0\\ 0 \end{bmatrix}, \begin{bmatrix} 1 & 0.5\\ 0.5 & 1 \end{bmatrix} \right). \end{align}\)

Add n_mis=500 more rows of data. Y and X are correlated so that knowing one is informative of the other, but both are missing in rows 501–1,000.

Next generate Z ~ Bern(0.5) in all n_obs+n_mis=1,000 rows. Note that Z contains no information beyond its own marginal distribution. Y and X are measurements on (simulated) patients – states of nature, if you like. Let’s say Z represents a treatment decision in a randomised trial. This is under the research team’s control and, with non-dynamic randomisation methods, we can prepare a randomisation list up-front for as many potential future patients as we like, but it contains no information relating to the states of nature. The way I’ve generated Z mimics this: we have a list prepared for up to 1,000 participants and recruit 500.

Estimands

Let’s keep it simple and consider the following two estimands:

1. β_X in the regression of Y on X. Its true value is β_X=ρ(σ_Y/σ_X)=0.5(1/1)=0.5.

2. β_Z in the regression of Y on X and Z. Its true value is β_Z=0, because Z is uncorrelated with both Y and X.

Methods of analysis

In each of the below cases, we will use two substantive models of interest, one for each estimand:

1. Linear regression (OLS) of Y|X to estimate β_X.

2. Linear regression (OLS) of Y|X,Z to estimate β_Z.

The reason we’re using a model without Z to estimate β_X is I want it to be absolutely clear that the incomplete rows hold no data on either of the variables in the model. In (2), the incomplete rows all have Z observed, but they still contain no information about β_Z.

For each of these, we conduct three different analyses:

1. Full data analysis of the 500 observations with Y and X observed (the benchmark I’ll compare MI against).

2. Multiple imputation of the 500 empty rows, 5 imputations.

3. Multiple imputation of the 500 empty rows, 100 imputations.

I’ve included both 5 and 100 imputations because multiple imputation becomes more efficient as the number increases (see this post for more).

Since Y and X are always observed together or missing together, we have a so-called “monotone missingness” pattern. This means our imputation model need not be iterative, like a multivariate normal or chained equations. Instead we can just impute using a monotone procedure (e.g. impute X|Z, then Y|X,Z, then stop; or equivalently impute Y|Z, then X|Y,Z, then stop) and that’s much faster. For both X and Y, the imputation model will be linear regression imputation including Z as a covariate.

Performance measures

We’re primarily interested in relative precision compared with analysis of the full data. We want to know the gain in precision of an MI procedure relative to analysis of the full data (summarised as a %).

I mentioned above the fraction of missing information, and that fact that MI can estimate this. Let’s see how accurately it evaluates the information it is missing, shall we?

Implementation

Coded and run in Stata 18. The only user-written package is {simsum} (version 2.2.3), for analysis of simulation studies.

I started with an initial 800 repetitions then assessed Monte Carlo error, and decided that was sufficient. If you disagree, the code is on GitHub and you can increase the number of reps. Or if you don’t speak Stata, replicate it in your software of choice and add to the repo. Hey, if you do it before August I’ll acknowledge you in a talk (please do)!

Results

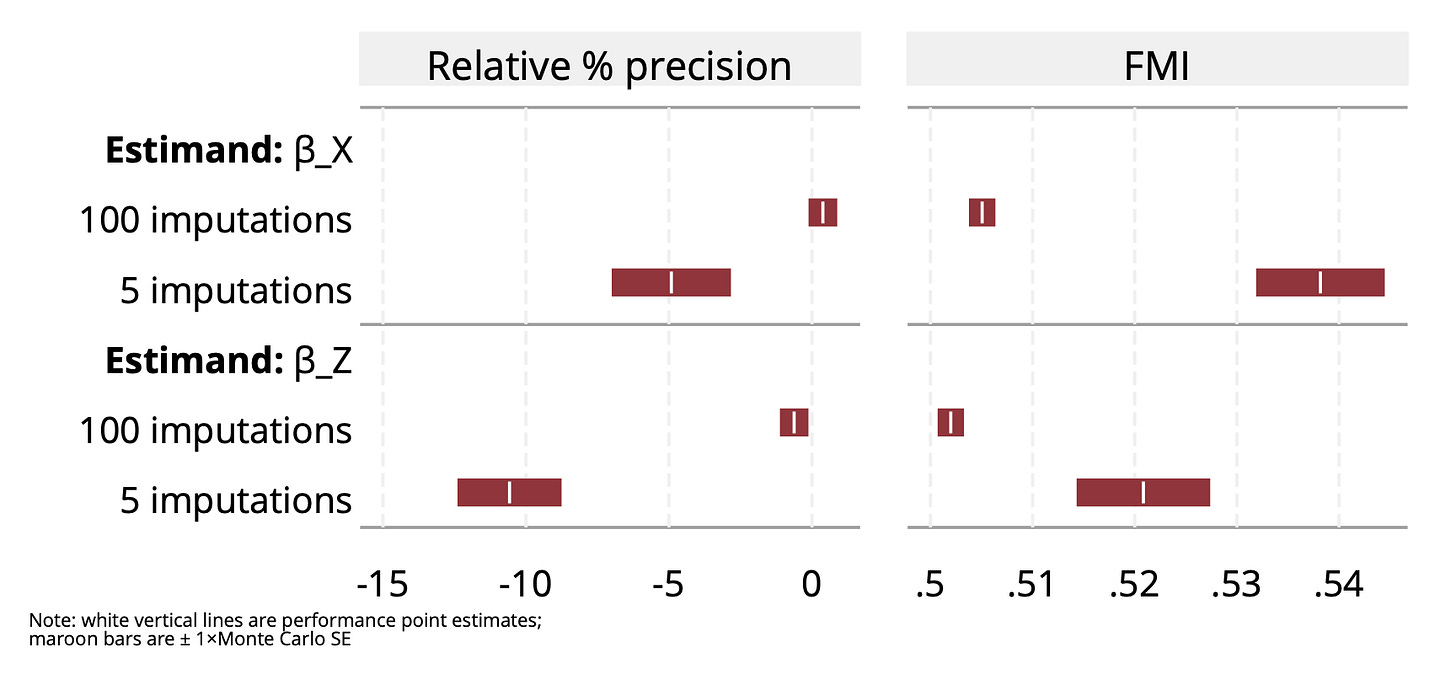
It’s wild that substack doesn’t have a table feature. Fine, have a figure!

The left panel shows relative % precision increase vs. full data analysis; the right shows the estimated fraction of missing information. The upper rows are results for β_X and the lower rows are for β_Z.

The results are roughly as I would expect. The left panel shows that relative precision gain is around 0 when we use a relatively large number (100) of imputations. We lose information when we use 5 imputations. We know that MI becomes more efficient as the number of imputations increases. What I don’t immediately see is why there is a difference in relative precision for the two estimands. Although the difference in relative precision appears compatible with Monte Carlo error, the Monte Carlo error of the difference in relative precisions is actually quite low because the results come from analysis of the same simulated datasets; see here. Do comment if you understand why!

The FMI results are worth looking at. Remember that FMI estimates the information missing compared to if we had full data. Relative precision showed that we lost almost nothing, yet the FMI is estimated at around a half (slightly more with just 5 imputations). Why? This is because MI had seen the “full” sample size as n=1,000 and compared its information to what it would have with n=1,000 fully observed rows, rather than the n=500, which was the actual sample size. So it’s projected information (which BTW is 1/variance) is based on half the variance of the n=500 case. In a sense, MI gets it right: it does have half the information it would have with n=1,000, and does not know that we artificially added 500 empty rows!

1. Heinze G, Boulesteix A-L, Kammer M, Morris TP, White IR. Phases of methodological research in biostatistics—Building the evidence base for new methods. Biometrical Journal. 2024; 66: 2200222. https://doi.org/10.1002/bimj.202200222

2. Schafer JL. Multiple imputation: a primer. Statistical Methods in Medical Research. 1999; 8(1): 3–15. doi:10.1177/096228029900800102

3. Carpenter JR, Bartlett JW, Morris TP, Quartagno M, Wood AM, Kenward MG (2023). Multiple Imputation and its Application 2e. Statistics in Practice. Boca Raton, Florida: Wiley. 2 ed.